 |
 |
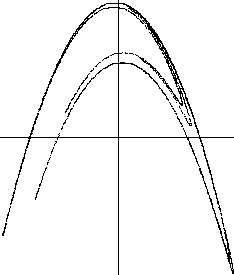
| x = [-0.4046, +0.4010] y = [-1.3490, +1.3370] |
x = [0.1500, 0.2500] y = [0.2600, 0.3600] |
 |
 |
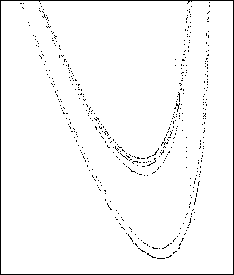
| x = [0.2070, 0.2200] y = [0.3020, 0.3100] |
x = [0.2103, 0.2110] y = [0.3050, 0.3055] |
Atractores Extraños
(ver el
caos en el cuerpo humano)
En muchas representaciones gráficas como las anteriores, representadas en diferente número de dimensiones, se observan zonas peculiares alrededor de determinados puntos. Ejemplo:
El atractor de
Henon con sucesivas ampliaciones:
f: (x, y) --> (0.3 y, 1 + x - 1.4 y2)
 |
 |
| x = [-0.4046, +0.4010] y = [-1.3490, +1.3370] |
x = [0.1500, 0.2500] y = [0.2600, 0.3600] |
 |
 |
| x = [0.2070, 0.2200] y = [0.3020, 0.3100] |
x = [0.2103, 0.2110] y = [0.3050, 0.3055] |
Otras gráficas de atractores extraños:
Lorenz (3D):
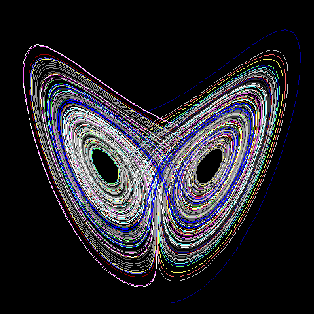
Ikeda (2D):

Ushiki (2D)

Los atractores extraños representan lo "extraño" en el impredecible comportamiento de sistemas caóticos complejos. (En sistemas simples los atractores suelen ser puntos). Como Escohotado en "Caos y Orden" señala, "La dinámica clásica enseña que cualquier trayectoria supone alguna fuerza, responsable del desplazamiento de tal o cual masa desde un lugar a otro. En contraste con ello, ciertos atractores dependen como cualquier sistema físico de limitaciones externas, pero reelaboran espontáneamente esos límites con cascadas de bifurcaciones, que acaban resolviéndose en alguna fluctuación interna triunfante. A diferencia de los sistemas inerciales, ese tipo de existencia elige hasta cierto punto su evolución, incluyendo algo configurador más parecido a los genes, que está animado y no se despliega en una sino en todas direcciones. El modelo lineal empieza y termina por la predicción, idealizando constantemente su contenido, mientras los atractores son extraños o caprichosos, aunque llevan en sí cierta forma que se autoproduce; cada uno de sus momentos va inventándose, y desde esa libertad/necesidad que es su caos "atrae" constantemente algo afín (nunca igual, nunca distinto) a una particular existencia."
https://elcaos.tripod.com/