Escalas y
dimensiones fractales
Escalas. Es propio de
los fractales que se encuentren autosemejanzas a diferentes
escalas (ver ampliación de un fractal.) Esta propiedad también es aplicable al mundo
natural (ver el caos en la naturaleza.) Por ejemplo, en la microescala de nuestra
existencia, cada uno de nosotros es una única representación
del mundo que nos ha creado. Por eso es adecuado que, en las
primeras semanas después de la concepción, un feto pase a través
de formas que recuerdan al pescado, a los anfibios y a otros mamíferos,
atravesando una microhistoria del caos de la evolución hasta que
encuentra su propia forma y su propio rostro.
Dimensiones. Si
cogemos una línea (una dimensión) y la arrugamos, se puede
decir que obtenemos un plano, puesto que la línea ya no tiene
una sóla dimensión, aunque tampoco tiene dós: está a medias.
De igual forma, si cogemos un papel hacemos una bola, tenemos
algo que está a medias entre dos y tres dimensiones.
Precisamente este es el caso de los fractales. Veamos un ejemplo:
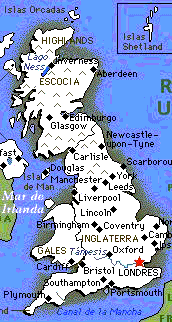 La costa británica, como toda forma natural es un
fractal (de dimensión fractal 1,26). Suponiendo que se
encontrara en el plano, hagamos el experimento de medir la
longitud de su costa. Hacemos una foto desde un satélite y
medimos la periferia. Obtenemos determinado número de kilómetros,
pero si hacemos la foto desde un avión, veremos que aparecen más
detalles de la costa y, al volver a medir, obtenemos un número
mayor. Si seguimos ampliando y midiendo cada vez mayor número de
detalles, la longitud seguirá aumentando hasta que, suponiendo
que pudiéramos llegar a medir con infinito número de detalles,
la longitud de la costa resultaría ser muchísimo más larga que
la que fue medida con pocos detalles.. ¿Por qué? Porque la línea
costa no se puede medir como algo unidimensional, pero tampoco
llega a ser bidimensional. Está en medio.
La costa británica, como toda forma natural es un
fractal (de dimensión fractal 1,26). Suponiendo que se
encontrara en el plano, hagamos el experimento de medir la
longitud de su costa. Hacemos una foto desde un satélite y
medimos la periferia. Obtenemos determinado número de kilómetros,
pero si hacemos la foto desde un avión, veremos que aparecen más
detalles de la costa y, al volver a medir, obtenemos un número
mayor. Si seguimos ampliando y midiendo cada vez mayor número de
detalles, la longitud seguirá aumentando hasta que, suponiendo
que pudiéramos llegar a medir con infinito número de detalles,
la longitud de la costa resultaría ser muchísimo más larga que
la que fue medida con pocos detalles.. ¿Por qué? Porque la línea
costa no se puede medir como algo unidimensional, pero tampoco
llega a ser bidimensional. Está en medio.
Una cuestión
interesante sería si realmente existen las dimensiones o es
nuestra forma de pensar la que las ha inventado. Está claro que
el mundo también podría ser medido con otros ejes de
coordenadas diferentes a los que solemos utilizar. Podríamos
clasificar las cosas dentro de dimensiones curvas o espirales. Sólo
que tendríamos que modificar nuestras ecuaciones geométricas y
temporales. Tal vez estemos clasificando todas las formas que nos
vienen a la cabeza dentro de un sistema de dimensiones lineales,
porque esa cosa llamada línea fue lo primero que nos vino a la
cabeza. Una línea es una especie de simplificación excesiva :
al imaginar un objeto de exáctamente una dimensión estamos
haciendo una simplificación de las dimensiones (ya que nada
tiene exáctamente una dimensión), por otro lado al imaginar una
línea perfectamente recta estamos haciendo una simplificación
de la realidad, donde no existen líneas simples. ¿Cómo
imaginaríamos la realidad si la forma que utilizamos como
sistema de referencia hubiera sido diferente de lo que hoy
llamamos línea recta?
(Ver ¿es el
mundo diferenciable? , La no-linealidad
del Tiempo y ¿Existen las
formas?)
https://elcaos.tripod.com/
 La costa británica, como toda forma natural es un
fractal (de dimensión fractal 1,26). Suponiendo que se
encontrara en el plano, hagamos el experimento de medir la
longitud de su costa. Hacemos una foto desde un satélite y
medimos la periferia. Obtenemos determinado número de kilómetros,
pero si hacemos la foto desde un avión, veremos que aparecen más
detalles de la costa y, al volver a medir, obtenemos un número
mayor. Si seguimos ampliando y midiendo cada vez mayor número de
detalles, la longitud seguirá aumentando hasta que, suponiendo
que pudiéramos llegar a medir con infinito número de detalles,
la longitud de la costa resultaría ser muchísimo más larga que
la que fue medida con pocos detalles.. ¿Por qué? Porque la línea
costa no se puede medir como algo unidimensional, pero tampoco
llega a ser bidimensional. Está en medio.
La costa británica, como toda forma natural es un
fractal (de dimensión fractal 1,26). Suponiendo que se
encontrara en el plano, hagamos el experimento de medir la
longitud de su costa. Hacemos una foto desde un satélite y
medimos la periferia. Obtenemos determinado número de kilómetros,
pero si hacemos la foto desde un avión, veremos que aparecen más
detalles de la costa y, al volver a medir, obtenemos un número
mayor. Si seguimos ampliando y midiendo cada vez mayor número de
detalles, la longitud seguirá aumentando hasta que, suponiendo
que pudiéramos llegar a medir con infinito número de detalles,
la longitud de la costa resultaría ser muchísimo más larga que
la que fue medida con pocos detalles.. ¿Por qué? Porque la línea
costa no se puede medir como algo unidimensional, pero tampoco
llega a ser bidimensional. Está en medio.