Cómo se descubrió el caos en las matemáticas

Cuando una función se reitera muchísimas veces el resultado puede resultar casi imprevisible, dependiendo muy sensiblemente a cualquier variación del valor inicial.

Comprobaremos esto utilizando una función en una gráfica: (gráficos por Glenn Elert)

1. Dibujar dos curvas en los mismos ejes. Escoger un punto del eje X. Este punto será el valor inicial.
2. Dubujar una vertial desde ese punto hasta interceptar la parábola.
3. Dibujar una horizontal desde la intercepción hasta llegar a la línea diagonal.
4. Repetir paso 2 con el último punto obtenido.

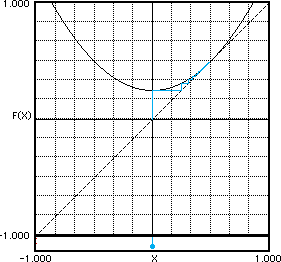
Parámetro: C= 1/4 para el valor inicial 0. La línea que se forma se llama órbita, y tiende a 1/2.

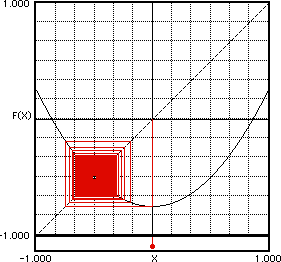
Parámetro = -3/4. Nótese que la órbita se aproxima desde los cuatro lados al punto, pero después de las 1000 iteraciones realizadas todavía queda un puntito blanco en el centro: la órbita no ha alcanzado su valor final.

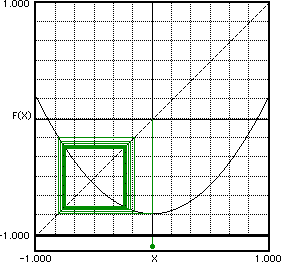
C= -13/16. La órbita comienza a circular alternándose entre -3/4 y -1/4.

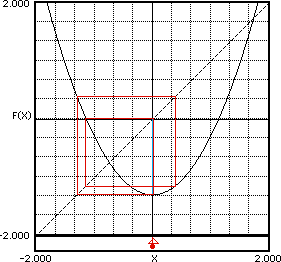
C= -1.3. La órbita oscila en un cilco cuádruple entre los valores 1.2996224637, 0.3890185483, -1.1486645691, y 0.0194302923, Esta vez después de sólo 100 iteraciónes la órbita parece haber alcanzado su valor final.

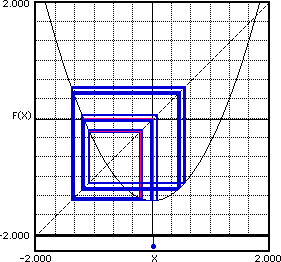
C= -1.4015. Se parece a la gráfica anterior, sin embargo en ésta la óribta nunca pasa por el mismo sitio sino que se ajusta a unas bandas.

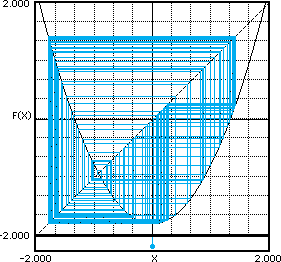
C= -1.8. Esto es el CAOS! Se ve que al cambiar el valor inicial (por pequeño que sea el cambio) la órbita cambia totalmente.

(Ver Diagramas de bifurcación)

https://elcaos.tripod.com/